Activities│Fujisawa Laboratory│Institute of Mathmatics for Industry, Kyushu University

Activities

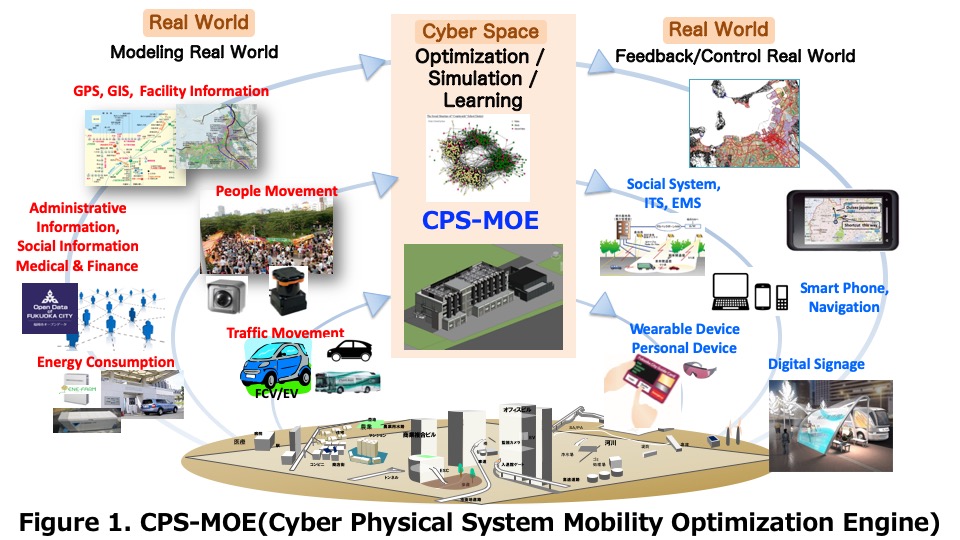
Cyber-Physical System Mobility Optimization Engine (Figure 1)
In recent years, various efforts have been made to realize a so-called super-smart society that is safe, secure, and convenient by combining and fusing the latest technologies worldwide. The research collaborations between academic and industrial institutions are not enough; however, there are a few research projects aimed at making cross-sectoral and simultaneous solutions from mathematical theory to ecosystem construction into actual services. Our research can cover the construction and verification of the organization for the fusion of various fields. Our project team has also developed the Cyber-Physical System Mobility Optimization Engine (CPS-MOE) that provides various functions inclusive of creating new industries, reducing cost and industrial waste, and constructing sets of services for calculation of the optimum control schedule of transportation agencies. CPS-MOE includes graph analysis, optimization algorithms, etc., and the following describes our works on them.

Graph Analysis (Figure 2)
The extremely large-scale graphs that have recently emerged in various application fields, such as transportation, social networks, cyber-security, and bioinformatics, require fast and scalable analysis. The large-scale graph analysis has attracted significant attention as a new application of the next-generation supercomputer. We have advanced the development of the software package that performs high-speed processing of large-scale graphs. Our project team combined highly advanced software technologies as follows;
1: Algorithms to reduce redundant graph searches,
2: Optimization of communication performance on massively parallel computers connected by thousands to tens of thousands of high-speed networks,
3: Optimization of memory access on multicore processors.
They finally succeeded in coping with large-scale and complicated real data expected in the future and developing graph search software with the world’s highest performance. From 2014 to 2020, our project team has been a winner at the Graph500 benchmark(https://graph500.org), which is designed to measure the performance of a computer system for applications that require irregular memory and network access patterns.

Mathematical optimization (Figure 3)
We also present our parallel implementation for large-scale mathematical optimization problems. The semidefinite programming (SDP) problem is one of the most predominant problems in mathematical optimization. The primal-dual interior-point method (PDIPM) is one of the most powerful algorithms for solving SDP problems, and many research groups have employed it for developing software packages. However, two well-known major bottleneck parts (the generation of the Schur complement matrix (SCM) and its Cholesky factorization) exist in the algorithmic framework of PDIPM. We have developed a new version of SDPARA, which is a parallel implementation on multiple CPUs and GPUs for solving extremely large-scale SDP problems that have over a million constraints. SDPARA can automatically extract the unique characteristics from an SDP problem and identify the bottleneck. When the generation of SCM becomes a bottleneck, SDPARA can attain high scalability using a large quantity of CPU cores and some techniques for processor affinity and memory interleaving. SDPARA can also perform parallel Cholesky factorization using thousands of GPUs and techniques to overlap computation and communication if an SDP problem has over two million constraints and Cholesky factorization constitutes a bottleneck. We demonstrate that SDPARA is a high-performance general solver for SDPs in various application fields through numerical experiments at the TSUBAME 2.5 supercomputer, and we solved the largest SDP problem (which has over 2.33 million constraints), thereby creating a new world record. Our implementation also achieved 1.774 PFlops in double precision for large-scale Cholesky factorization using 2,720 CPUs and 4,080 GPUs.

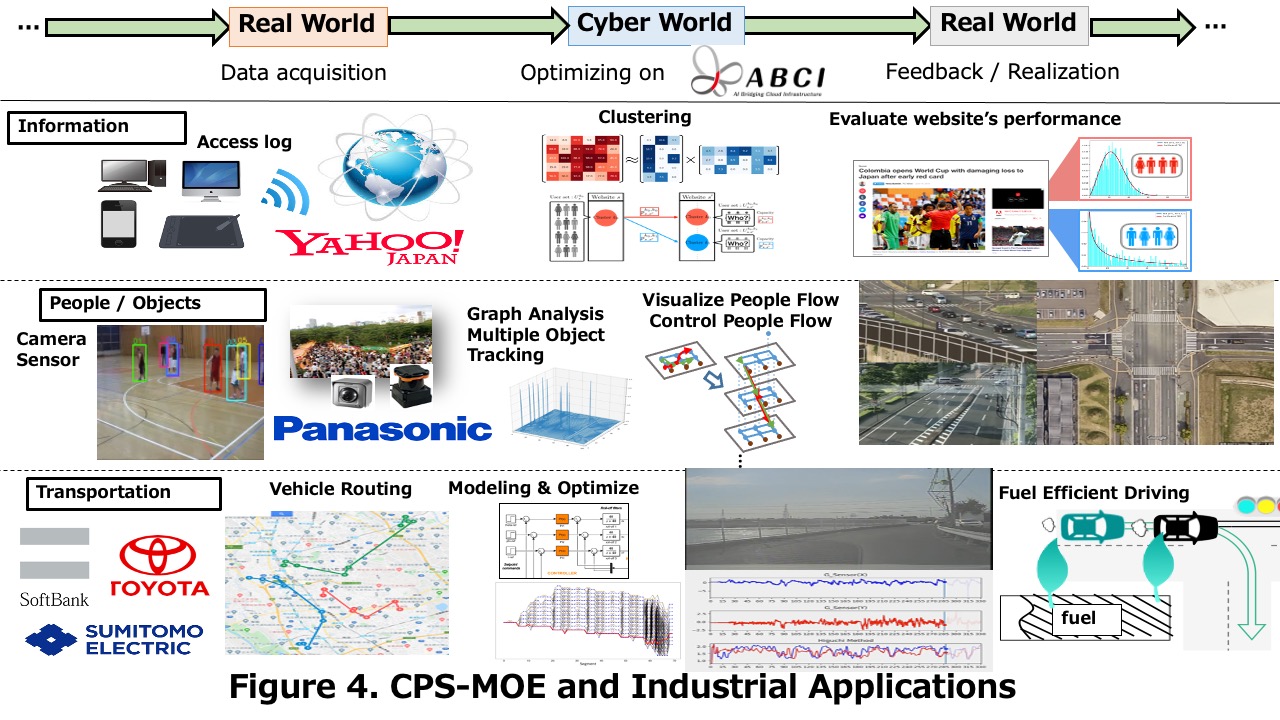
Applications of CPS-MOE (Figure 4)
To realize the industrial applications of CPS-MOE, we have devoted our efforts to the proposal and development of new mathematical and information technologies to represent, predict, optimize, and control the following three mobilities.
1. Mobility of human and object: location information acquisition and tracking (Deep learning), congestion detection and flow optimization, and visualization (with Panasonic from 2016).
2. Mobility of information (human interest and intention): User clustering based on page transition and intention (with Yahoo! Japan from 2017).
3. Mobility of traffic (optimum automatic operation): MaaS (Vehicle Routing), Automatic operation within the area (road-vehicle cooperative driving system) + optimum control system (Minimization of fuel consumption on power train simulator) (with Softbank from 2020 and Toyota motor and Sumitomo Electronic from 2017).
By collaborating with the private companies, they construct virtual “shops,” “factories,” “ warehouses,” among others. In cyberspace using various types of actual data and eventually improve the service level and verify the effects of the reduced cost in real space. It can be expected to contribute significantly to the promotion of Sustainable Development Goals (SDGs), especially Goals 9 and 11. It also makes it possible to build a society that ensures the movement in a free and safe space for all people. Additionally, it is expected to create industries that offer the following new services, so they can accelerate promotion by transferring technology to participating private companies.